Combinatorial Geometry Minimum Number of Line Segments at Right Angles to Start and Return to Origin

Question No. 25 of the ASMO  (Math Olympiad) in Image

 

 

 

 

 

 

A Possible Solution

 

 

 

To Get a sum of zero, we need a minimum of 8 addends from the Counting Numbers 1 to 9 as described as follows:

 

 

Up or Down 2, 4, 6, 8,

 

 

Where positive is “up” and negative is “down”

 

Since

 

 

2 + 8 + (-4) + (-6) = 0

 

 

 

 

Similarly

 

Left or Right: 1, 3, 5, 7

 

1 + 7 + (-3) + (-5) = 0

 

 

Where positive is “right” and negative is “left”

 

 

 

What can we say?

 

Movement for line segments are as follows:

 

 

2 , 8 —-> both “up”

 

 

(-4) + (-6) —> both “down”

 

 

Likewise:

 

1 , 7 —-> both “right”

 

(-3) , (-5) —> both “left”

 

 

 

 

 

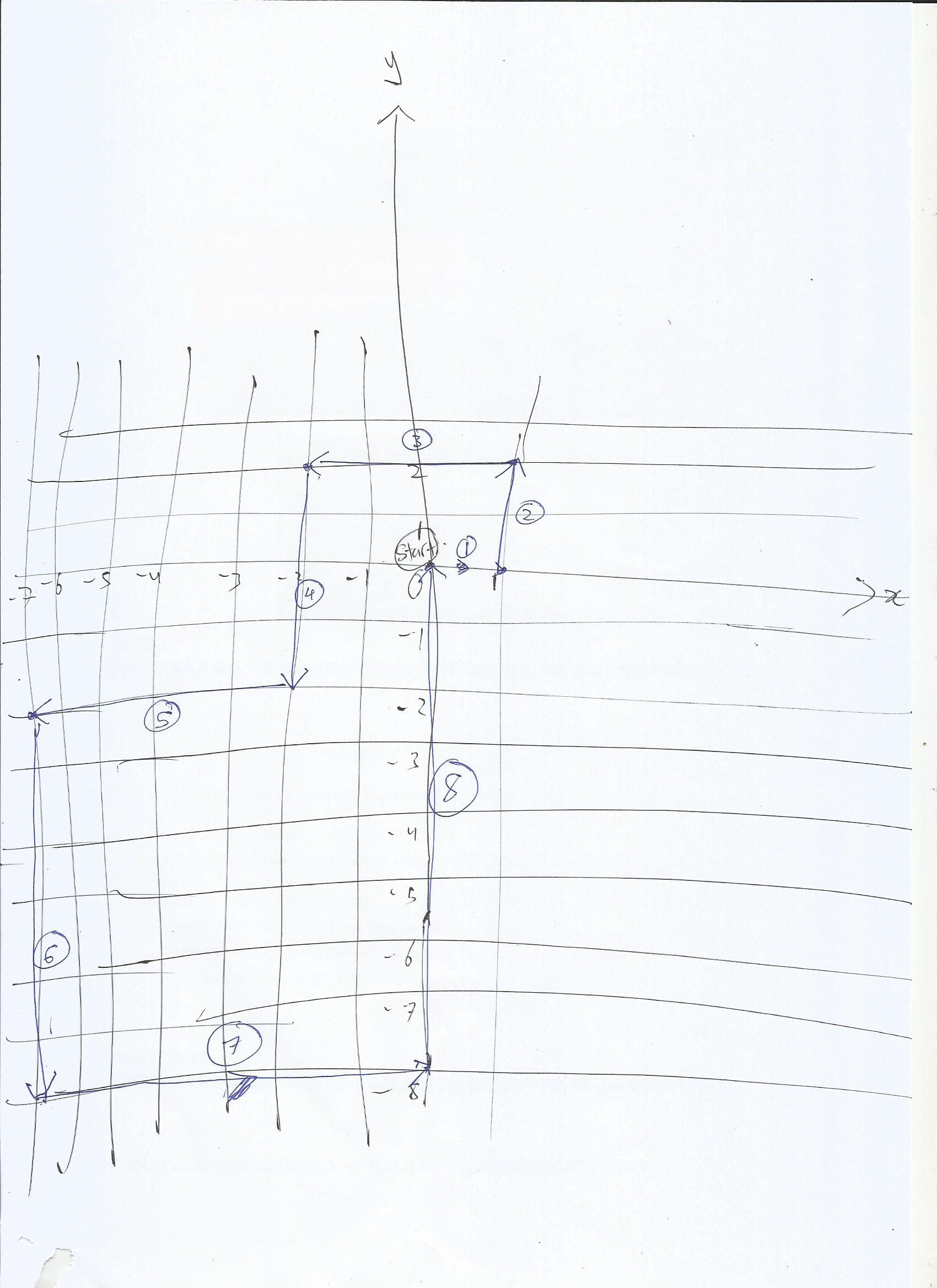
So, a Solution is

 

Start at (0, 0)

 

Move right 1 unit (1, 0)

 

Move up 2 units (1, 2)

 

Move left 3 units (-2, 2)

 

Move down 4 units (-2, -2)

 

Move left 5 units (-7, -2)

 

Move down 6 units (-7, -8)

 

Move right 7 units (0, -8)

 

Move up 8 units (0, 0)

 

 

 

 

There are exactly 8 segments in the shortest possible path as described above (Answer).

 

 

 

P/S: Here’s a Pictorial Sketch that the Solution above Works

 

Please pardon the horrible handwritten sketch , LOL