Geometry Arc Circle Area

I Found this Interesting Math Olympiad PUTNAM Problem and Its Solution (not mine) whilst browsing.

.
.
.

A Comment for edification

A Very Clever Solution you have there.

Comment: Why Multiply by 2?

(i) Twice the First Picture in Addend

Note that

“First Picture in Addend” = (Area of Triangle) = (half of area of Top Left Rectangle)

Thus doubling it,

“Twice the First Picture in Addend” = Twice (half of area of Top Left Rectangle) = (Area of Top Left Rectangle)

(ii) Twice the Second Picture in Addend

Note that

“Second Picture in Addend” = (Area of Triangle) = (half of area of Bottom Right Rectangle)

Thus doubling it,

“Twice the Second Picture in Addend” = Twice (half of area of Bottom Right Rectangle) = (Area of Bottom Right Rectangle)

(iii) Twice the Third Picture in Addend

Note that

“Third Picture in Addend” = (Area of part-Arc)

Thus doubling it,

“Twice the Third Picture in Addend” = Twice (Area of part-Arc) = (Area of part-Arc COUNTED TWICE, one for its calculation in A and the other for its calculation in B.)

Yes only this area is counted “twice” in the Overall Sum because it occurs in both “A and B respectively” .

(iv) Total Shaded Area

(Total Shaded Area) or (A + B.)

= 2 x [ (half of area of Top Left Rectangle) + (half of area of Bottom Right Rectangle) + (Area of part-Arc)]

= 2 x [ Area of Arc with angle “theta” & radius “1”]

= 2 x [ (1/2) x r^2 x (theta) ], radius given as 1

= 2 x [ (1/2) x 1^2 x (theta) ]

= 2 x (1/2) x (theta)

= (theta)

= s

Depending only on the arc length s, when radius is given as claimed.

QED

Note:

Using (theta) in Radians,

r = radius = 1

(theta) = angle in Radians

s = arc length

Then,

s = r (theta)

s = (1) (theta)

s = (theta) which was substituted in the last line above.

P/S: A Visual Geometrical Proof  for the infamous elementary trigonometric identities

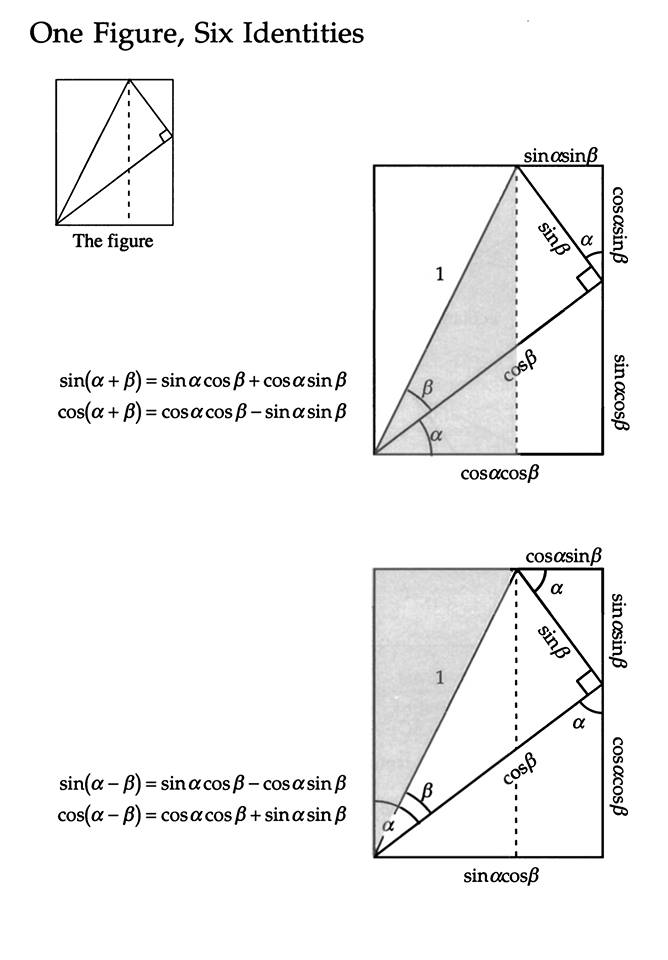
How to understand the proof above?

It’s difficult to explain here. Here are some useful pointers:

Example: Look at shaded triangle in Second Picture above.

Sin (a + b)

= (Vertical dotted line)/ (Hypotenuse)

= (Cos a Sin b + Sin a Cos b) / 1

= (Cos a Sin b + Sin a Cos b)

Can you see it?

Note:

(Vertical dotted line) = (Cos a Sin b + Sin a Cos b)

By diagram construction.

Example: In the right triangle with angle “a” in the Top Right Corner,

It has (hypotenuse) = Sin b

and an ‘angle a’.

So, its

Sin a = (‘horizontal length’)/(hypotenuse)

Sin a = (‘horizontal length’)/(Sin b)

So, rewriting this we obtain:

(‘horizontal length’) = (Sin a) x (Sin b) as shown in Pic etc.