A Tough Geometry Problem
Question
Triangle ABC has AC = BC, angle(ACB) = 96 degrees. D is a point in triangle ABC such that
angle(DAB) = 18 degrees and angle(DBA) = 30 degrees. What is the measure (in degrees) of
angle(ACD)?
Solution
The key in such geometry problems is to note the given values. It might just be (as it is in this problem) that these given values may have certain special properties which in turn may help to unlock further geometrical constraints (hidden) that can eventually help us solve the given problem.
We proceed as follows:
(i) Use the given value of 96 degrees {angle (ACB)} to find the value of angle(ABC)
angle(ABC) = 180 – angle(ACB) – angle(BAC) [angles in triangle ABC]
angle(ABC) = 180 – angle(ACB) – angle(ABC) [Triangle ABC is isosceles since given that AC = BC]
angle(ABC) = 180 – 96 – angle(ABC) [We’re also given that angle(ACB) = 96 degrees]
angle(ABC) + Angle(ABC) = 180 – 96 [Algebraic re-writing]
2 x angle(ABC) = 84 [Evaluating 180 – 96 = 84]
angle(ABC) = 84 ÷ 2 [Numerical re-writing]
angle(ABC) = 42 …(i) [Evaluating that 84 ÷ 2 = 42 degrees]
(ii) The given value of 96 degrees {angle (ACB)} is also interesting simply because its complementary value (in a straight line) is 180 – 96 = 84 degrees … (ii)
(iii) Now, the value of 84 degrees {found in (ii)} is of interest to us simply because it is twice the value found in (i) above.
That is, 84 = 42 x 2
What then? How is this information useful to us?
To unlock the usefulness of this fact, we have to extend the line BC (in that direction) to a point E such that BC = CE. Hence, we obtain the following diagram:
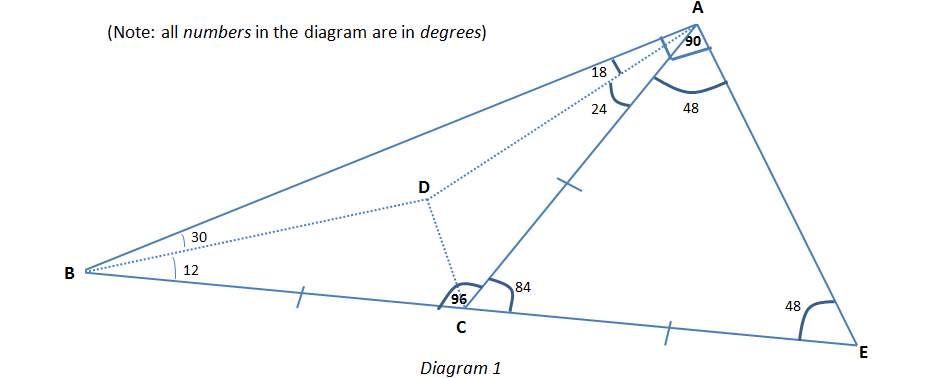
(iv) By obtaining the diagram above (due to the extension drawn to point E),
We note the interesting relationship between two particular angles in Diagram 1:
angle(ABC) = 30 + 12 = 42 degrees.
angle(ACE) = 84 degrees.
Since 84 = 2 x 42, we have the following relation:
angle (ACE) = 2 x angle(ABC)
Based on the relation above {angle (ACE) = 2 x angle(ABC)}, the following hidden geometrical property comes to light:
“angle at the centre of a circle is twice the angle at its circumference”
In other words, since the converse is also true (mathematically), we have:
“Points A, B and E lie on a circle centred at C”
*end of exploration*
Let’s get back to the question:
“Does the above help us to solve the problem? Do we really need the facts above to solve it?”
Unfortunately, No!
Thus it is with Mathematics; sometimes the exploration of a problem often reveals hidden properties but it may not necessarily help solve it (and neither it is required for its solution).
To solve the problem, we employ trigonometry (Sine Rule) on two triangles found in diagram 1.
These triangles are (the values contained therein are the angles):
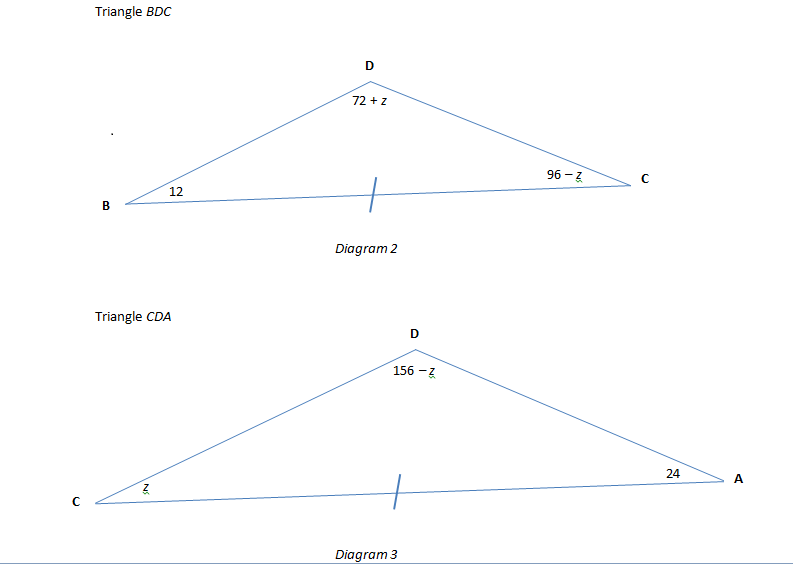
Do take note that in order to obtain the angles in the diagrams (2 & 3) above with respect to z or equivalently, in terms of z, we may do as shown below:
Firstly, define z = angle(ACD) = which is what we wish to find!
Next, in triangle DBC:
angle(BDC) = 180 – angle(DBC) – angle(BCD) [Using sum of angles in triangle DBC]
angle(BDC) = 180 – 12 – angle(BCD) [found earlier that angle(DBC) = 12 degrees]
angle(BDC) = 180 – 12 – {96 – z} [since angle(BCD) = 96 – z; by definition]
angle(BDC) = 72 + z [after simplifying 180 – 12 – 96 = 72]
Now, we proceed similarly with triangle CDA:
angle(CDA) = 180 – angle(CAD) – angle(ACD) [Using sum of angles in triangle CDA]
angle(CDA) = 180 – 24 – angle(ACD) [found earlier that angle(CAD) = 24 degrees]
angle(CDA) = 180 – 24 – z [since angle(ACD) = z; by definition]
angle(CDA) = 156 – z [after simplifying 180 – 24 = 156]
Crucially, we employ the Sine Rule to solve the problem as follows (all values are in degrees!):
In triangle BDC [Sine Rule yields]:
[BC] ÷ [Sin (72 + z)] = [DC] ÷ [Sin 12]
We get (after simplifying),
BC = { [DC] x [Sin (72 + z)] } ÷ [Sin 12] … (1)
Similarly, in triangle ADC [Sine Rule yields]:
[AC] ÷ [Sin (156 – z)] = [DC] ÷ [Sin 24]
We obtain (after simplifying),
AC = { [DC] x [Sin (156 – z)] } ÷ [Sin 24] … (2)
We also note the facts:
BC = AC (given in the problem) …(3)
Sin 24 = 2 Sin 12 Cos 12 …(4) [Using the Double angle formula, Sin 2A = 2 Sin A Cos A]
Using (1), (2) and (3), we can see that:
BC = AC
{ [DC] x [Sin (72 + z)] } ÷ [Sin 12] = { [DC] x [Sin (156 – z)] } ÷ [Sin 24]
After some simplifying,
Sin (72 + z) = Sin (156 – z) ÷ [2 Cos 12]
Now let x = 72 + z (to ease calculation).
(Note: This means z = x – 72 and 156 – z = 156 – (x – 72) = 156 – x + 72 = 228 – x)
So, the above becomes:
Sin x = Sin (228 – x) ÷ [2 Cos 12] …(5)
Subsequently, we employ:
Sin (M – N) = Sin M Cos N – Cos M Sin N by setting M = 228 and N = x, to get:
Sin (228 – x) = Sin 228 Cos x – Cos 228 Sin x
Sin (228 – x) = (– 0.74314) Cos x – (– 0.66913) Sin x
Sin (228 – x) = (– 0.74314) Cos x + (0.66913) Sin x
So,
Sin (228 – x) ÷ [2 Cos 12] = (– 0.74314 / [2 Cos 12] ) Cos x + (0.66913 / [2 Cos 12] ) Sin x
Sin (228 – x) ÷ [2 Cos 12] = (– 0.37987) Cos x + (0.34204) Sin x … (6)
Putting (6) into (5) to yields,
Sin x = (– 0.37987) Cos x + (0.34204) Sin x
(1 – 0.34204) Sin x = (– 0.37987) Cos x
0.65796 Sin x = (– 0.37987) Cos x
(Sin x ÷ Cos x) = (– 0.37987) ÷ 0.65796
Hence,
Tan x = (– 0.5773) [because Sin x ÷ Cos x = Tan x]
x = Tan-1 (– 0.5773) [Note that acute angle = Tan-1 (0.5773) = 30 degrees]
x = 180 – 30 [because x is less than 180 degrees and arctangent is negative]
x = 150 degrees [only; other periodical values are rejected since we’re dealing with
an angle inside triangles!]
Finally, put back x = 150 into z = x – 72 = 150 – 72 = 78 degrees; Remembering that z = angle(ACD),
Hence angle(ACD) = 78 degrees (answer).
*End*