Math Olympiad – A Visit to the Hong Kong Mathematical Olympiad HKMO 2015
Firstly, to avoid copyright problems we only are present solutions to a few selected (sample) questions from the Hong Kong Mathematical Olympiad HKMO 2015 . Also, each solution presented here is purely our work and we did not copy from the HKMO official solutions. This same is true for every Math Olympiad Problem found in this site.
Our solution may be used for “free” by both students and teachers alike in any way. Why?
“… Freely you received, freely give.” – Lord Jesus Christ (Matthew 10:8, NASB)
Our main aim is to allow needy and disadvantaged students to gain this knowledge which may be too costly or far from them in order that they too might compete in a fairer circumstance in regards to training obtained.
Someone remarked, ‘Instead of wasting your time doing this for free, why not increase your classes & earn more money and then give some to the poor?’
Reply, ‘Doing this way gives more. How? Please consider ‘wisely’ as follows:
If I earn only from a class, suppose I give away RM 30 to the poor from this earning after discussing all these questions in about 2 hours.
Compare now if I earn it there and also put it free here a little (can’t put too much due to copyright problem then as these organizations may be uncomfortable if I share too much of their stuff even if it is questions only). Not only I earn from it but other teachers may use it too for their bread + butter. Also, other students especially those poorer ones can also learn it too though they couldn’t afford the class nationwide or even globally.
If anyone says that they feel like I could have collected or given to the poor, here’s an encouragement: If you feel that you have benefited from the free materials on this site, please give some money to the poor/charity nearest to you and DO NOT tell us about it. We do not want to be an intermediate to the poor but prefer that you give directly to them wherever possible 🙂 .
Wanna see a Math regarding how this giving can actually be numerically enumerated?
Example: Suppose we had about 2000 unique visitor to our Math Olympiad Section where each benefited about 1 hour worth of Math Olympiad Class at say RM 100/hour. This means that we have ‘donated’ 2000 x 100 = RM 200, 000 = RM 200k worth of knowledge ‘freely’ which would be quite an impossible task if we were to rely on sharing only ‘manually via traditional classroom method’. Can you see it?
May God bless you as you share in your own way as we do in our own little way as well.
Let’s Begin.
Please note that the official solutions could be different. Math Olympiad problems may have more than 1 possible solution.
- Question 11 HKMO 2015
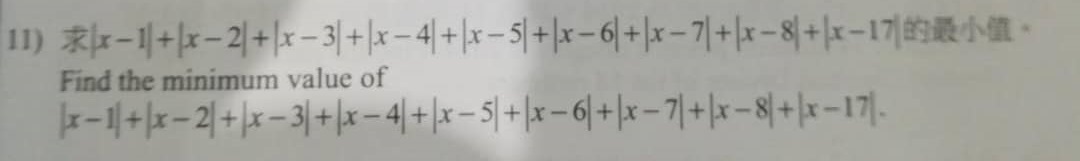
Solution
By Brute Force:
Minimum [x – 1] + … + [x – 8] + [x – 17]
Idea [x – b] = (x – b) if x >= b or (b – x) if x < b
Which b would make the above sum minimum?
Try x = 8,
Sum
= 7 + 6 + … + 1 + 0 + [8 – 17]
= 7(8)/2 + 9
= 28 + 9
= 37
Try x = 9
Sum
= 8 + 7 + … + 1 + [9 – 17]
= 8(9)/2 + 8
= 36 + 8
= 44
Try x = 10
Sum
= 9 + 8 + … + 2 + [10 – 17]
= 44 + 7
= 44 + 7
= 51
Increasing because (2 + …. + 8 + 9) = 44
Try x = 7,
Sum
= 6 + 5 + … + 1 + 0 +1 + [7 – 17]
= 6(7)/2 + 1 + 10
= 21 + 1 + 10
= 32
It is between 1 and 7
Try Middle x = 5
Sum
= 4 + 3 + … + 1 + 0 +1 + 2 + 3 + [5 – 17]
= 4(5)/2 + 3(4)/2 + 12
= 10 + 6 + 12
= 28
Beside
Try Middle x = 6
Sum
= 5 + 4 + … + 1 + 0 +1 + 2 + [6 – 17]
= 5(6)/2 + 3 + 11
= 15 + 3 + 11
= 29
Beside
Try x = 4
Sum
= 3 + 2 + 1 + 0 +1 + 2 + 3 + 4 + [4 – 17]
= 6 + 10 + 13
= 29
Hence, due to the Monotonic Nature of the Modulus Function for linear expression combinations at the ‘left & right’ of the ‘min/max point’, we may deduce that:
x < 3 —-> Sum > 29
x = 4 —–> Sum = 29
x = 5 —–> Sum = 28
x = 6 —–> Sum = 29
x > 6 —–> Sum > 29
Minimum x = 5, —> Minimum Sum = 28 (Answer)
2) Question 13 – Algebra
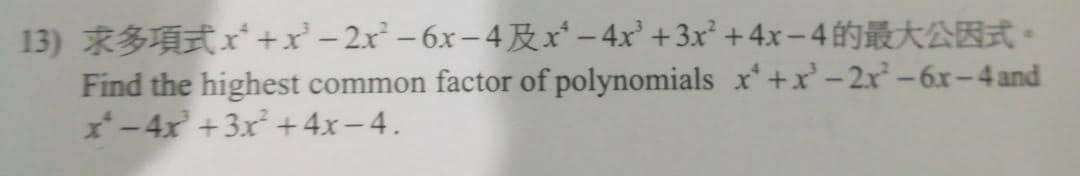
Solution
Let y be the common factor of the polynomials,
(x^4 + x^3 – 2x^2 – 6x – 4) and (x^4 – 4x^3 + 3x^2 + 4x – 4)
Idea
If numbers (algebraic expressions) a and b have common factor y
then y divides Sum = (a+b) and also Sum = (a – b)
And also
y divides Sum = (ra+ tb) and also Sum = (ma – nb) for any constants r, t, m, and n
Leading coefficient is 1 for x^4
Take y divides their difference
(x^4 + x^3 – 2x^2 – 6x – 4) – (x^4 – 4x^3 + 3x^2 + 4x – 4)
= 5x^3 – 5x^2 – 10x
= 5x (x^2 – x – 2)
Is (x^2 – x – 2) factorisable?
(x^2 – x – 2) = (x – 2) (x + 1)
So,
y is a factor of 5x (x – 2) (x + 1)
To check whether each of 5, x, (x – 2) and (x + 1) is a factor of the two given expressions separately, we use a Theorem

Use the Factor Theorem in Image
Let
f(x) = (x^4 + x^3 – 2x^2 – 6x – 4) and g(x) = (x^4 – 4x^3 + 3x^2 + 4x – 4)
Check
i. 5
the constant 5 is not readily a factor in both
ii. x
f(0) = (-4) and g(0) = (-4)
So x is NOT a factor or both
iii. (x – 2)
f(2) = (2^4 + 2^3 – 2(2)^2 – 6(2) – 4) = 0
and
g(2) = (2^4 – 4(2)^3 + 3(2)^2 + 4(2) – 4) = 0
So, (x – 2) is a factor of both
iv. (x + 1)
f (-1) = ([-1]^4 + [-1]^3 – 2[-1]^2 – 6[-1] – 4) = 0
and
g(-1) = ([-1]^4 – 4[-1]^3 + 3[-1]^2 + 4[-1] – 4) = 0
So, (x + 1) is a factor of both too
The highest common factor y
would be
y = (x +1)(x – 2) = (x^2 – x – 2) —> answer
Calculator approves this, link:
https://www.symbolab.com/solver/polynomial-long-division-calculator
For Function f(x) divided by y
f(x) = (x^4 + x^3 – 2x^2 – 6x – 4) = (x^2 – x – 2) [x^2 + 2x + 2]
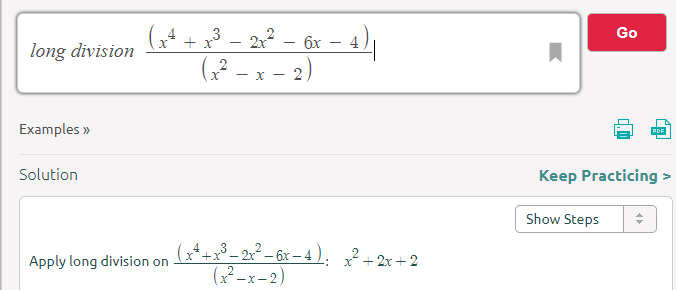
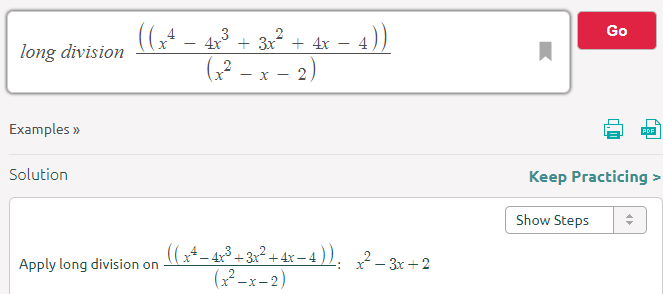
For Function g(x) divided by y
g(x) = (x^4 – 4x^3 + 3x^2 + 4x – 4) = (x^2 – x – 2) [x^2 – 3x + 2]
3) Question 13 – Geometry

Solution
DF = 5 and FC = 10
We use coordinate geometry:
Let D (0, 0) and so

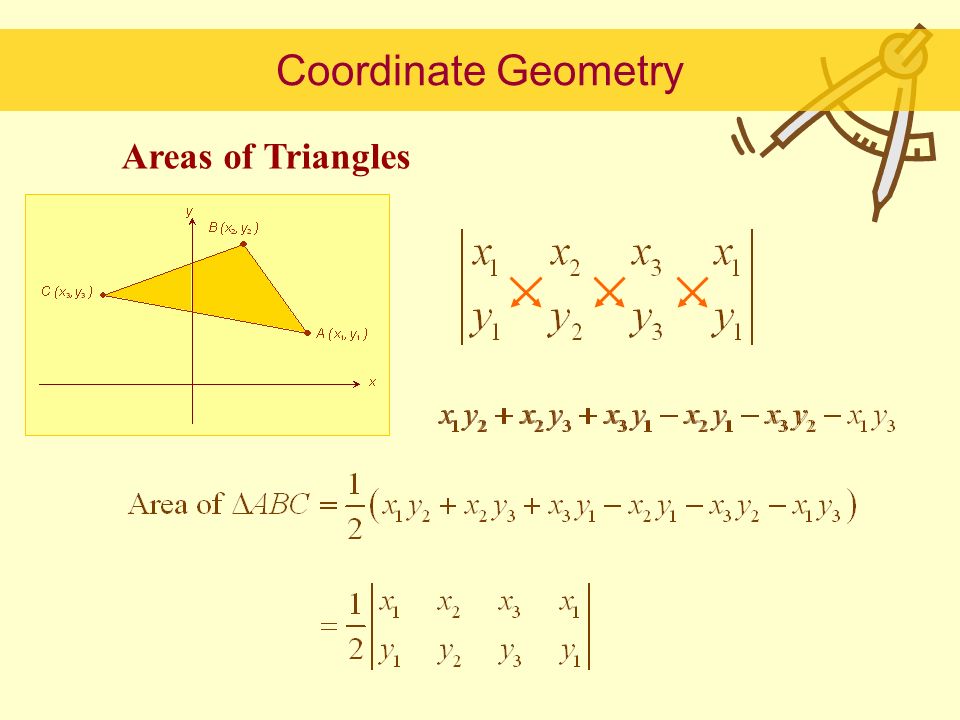
4) Question 16 – Inequalities
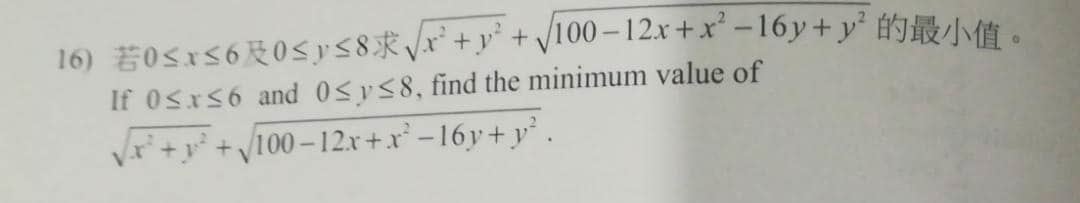
Solution
What does it mean?
Let the given expression be E.
So,
E = sqrt (x^2 + y^2) + sqrt (100 – 12x + x^2 – 16y + y^2)
E = sqrt (x^2 + y^2) + sqrt [(x – 6)^2 + (y – 8)^2]
Since x^2 + y^2 >= 0 + 0 = 0 and (x – 6)^2 + (y – 8)^2 >= (6 – 6)^2 + (8 – 8)^2 = 0 + 0 = 0
This means that we can either zero one part of it only. So which one? Two cases:
i. x^2 + y^2 = 0 , (x, y) = (0, 0)
E (min) = sqrt (0) + sqrt [(0 – 6)^2 + (0 – 8)^2] = sqrt (100) = 10
or
ii. (x – 6)^2 + (y – 8)^2 = 0, (x, y) = (6, 8)
E (min) = sqrt (6^2 + 8^2) + sqrt [(6 – 6)^2 + (8 – 8)^2] = sqrt (100) = 10
So, answer = 10 (either way using the idea that ‘real number squares are non-negative’).
5) Question 17 – Polynomials
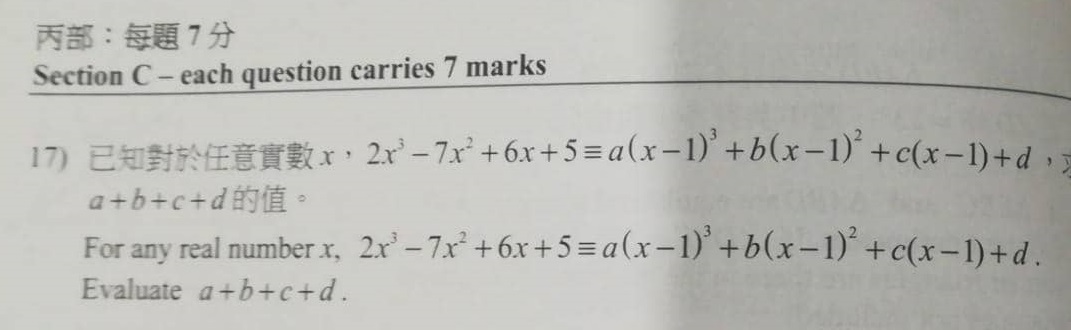
Solution
An Identity Question
An Algebraic Identity means that the Given Expression holds true for ‘any value of x’.
Given that
2x^3 – 7x^2 + 6x + 5 = a (x – 1)^3 + b (x – 1)^2 + c (x – 1) + d
Choose a ‘clever value for x’ which is ‘x = 2’.
Why? Because only then (x – 1) = (2 – 1) = 1
And so, we have
2(2)^3 – 7(2)^2 + 6(2) + 5 = a (2 – 1)^3 + b (2 – 1)^2 + c (2 – 1) + d
16 – 28 + 12 + 5 = a + b + c + d
5 = a + b + c + d
So,
(a + b + c + d) = 5 (answer)
6) Question 19 – Geometry of Area & Triangles
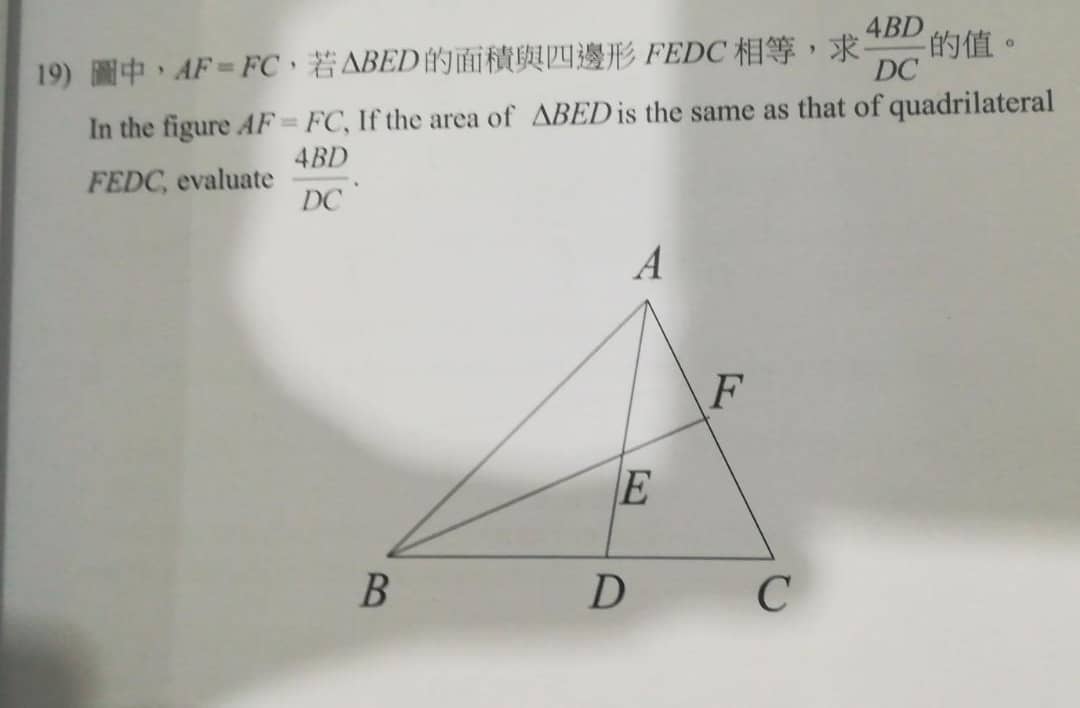
Solution (in 3 Images below)
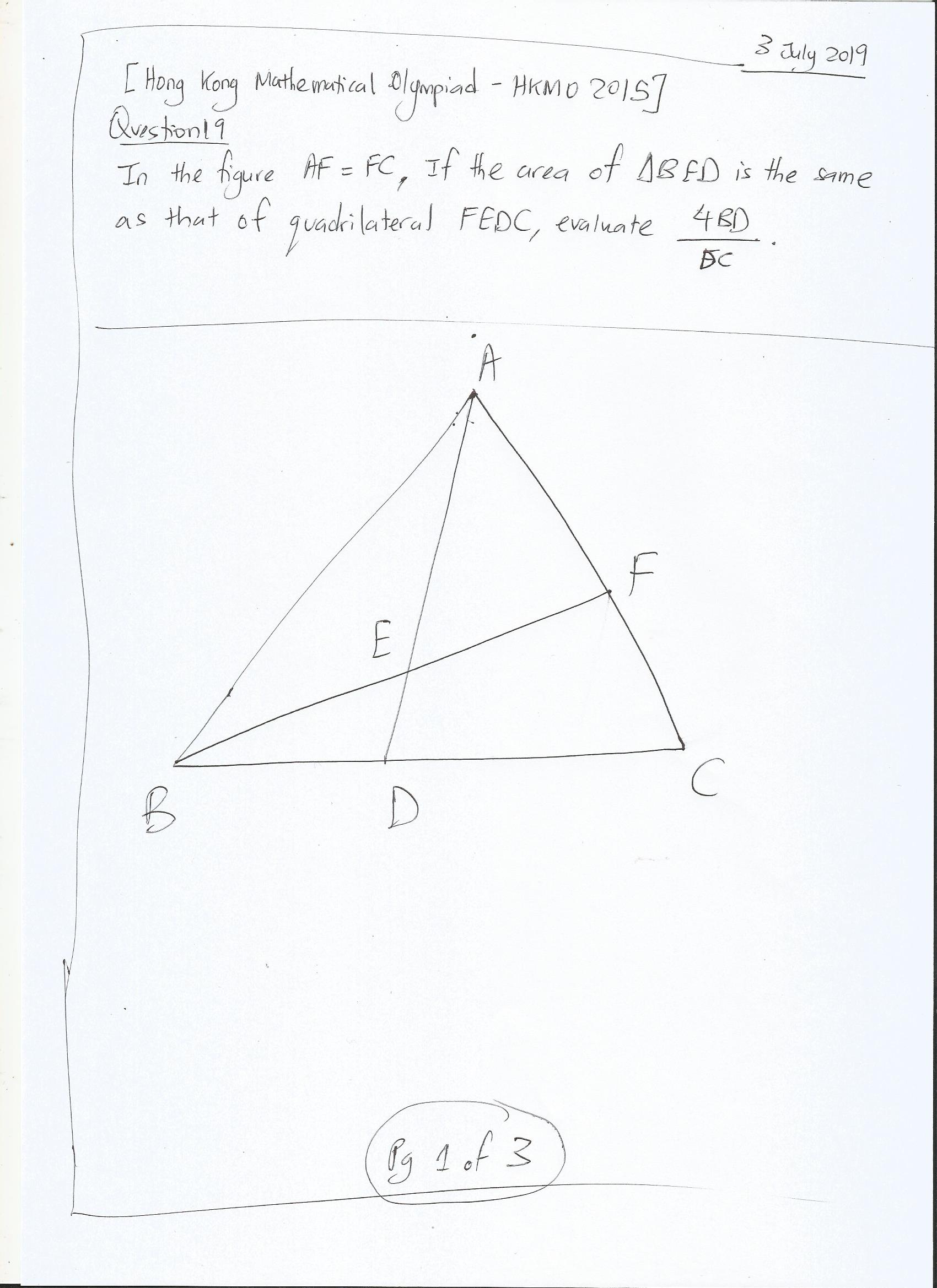


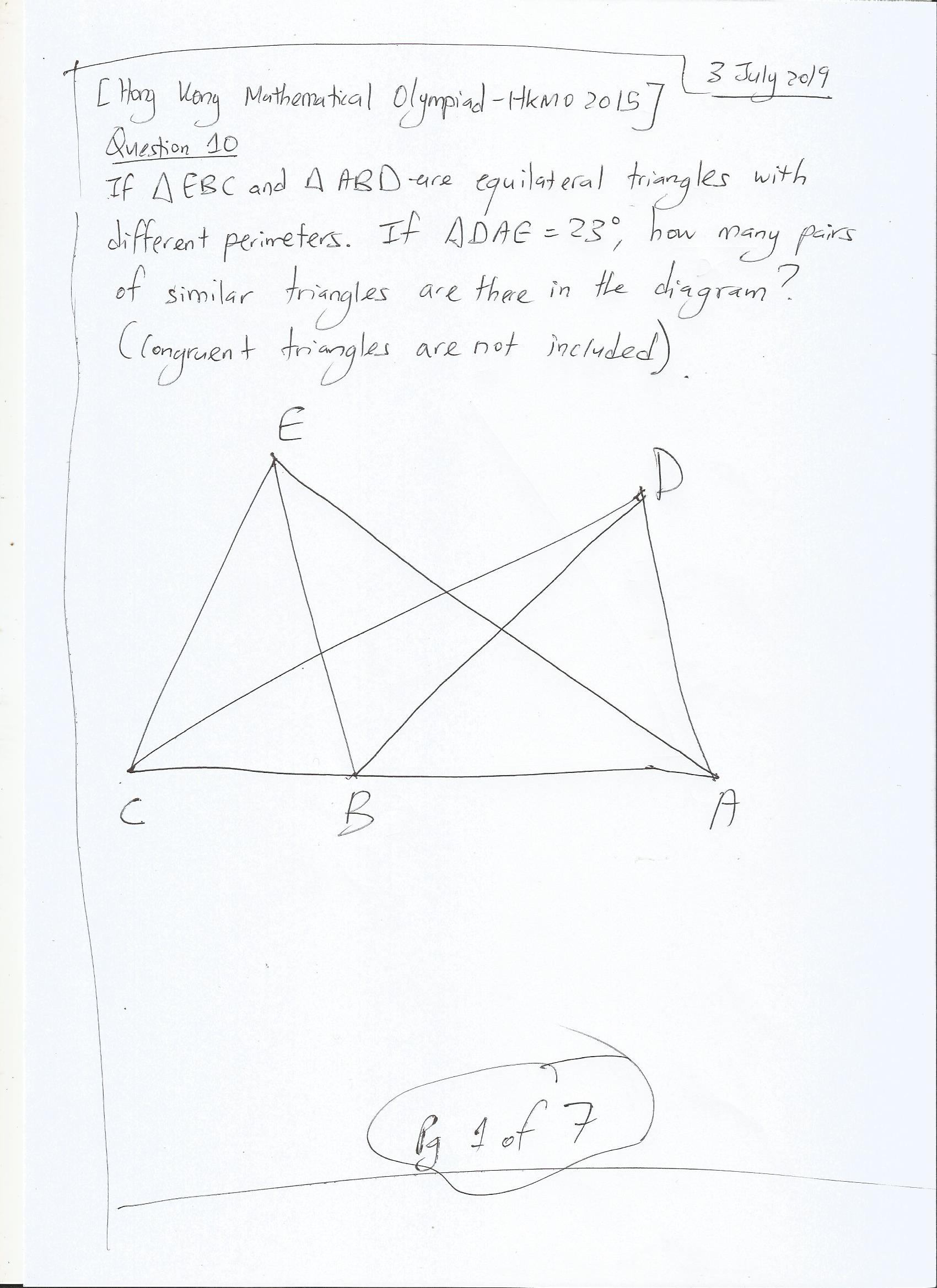
7) Question 10 – Geometry with a Trigonometric Depth with Similar Triangles

Solution (in 7 Images below)
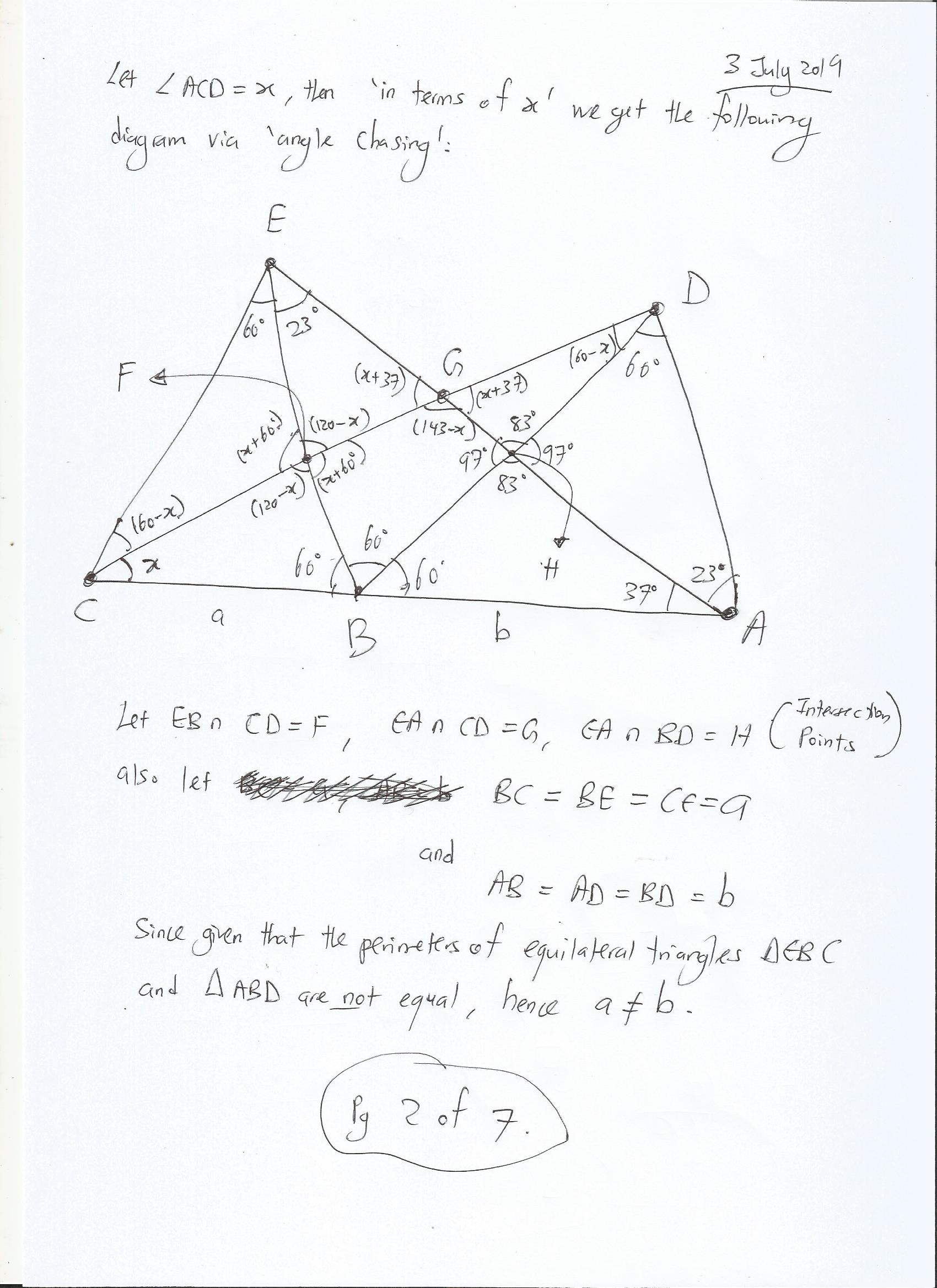



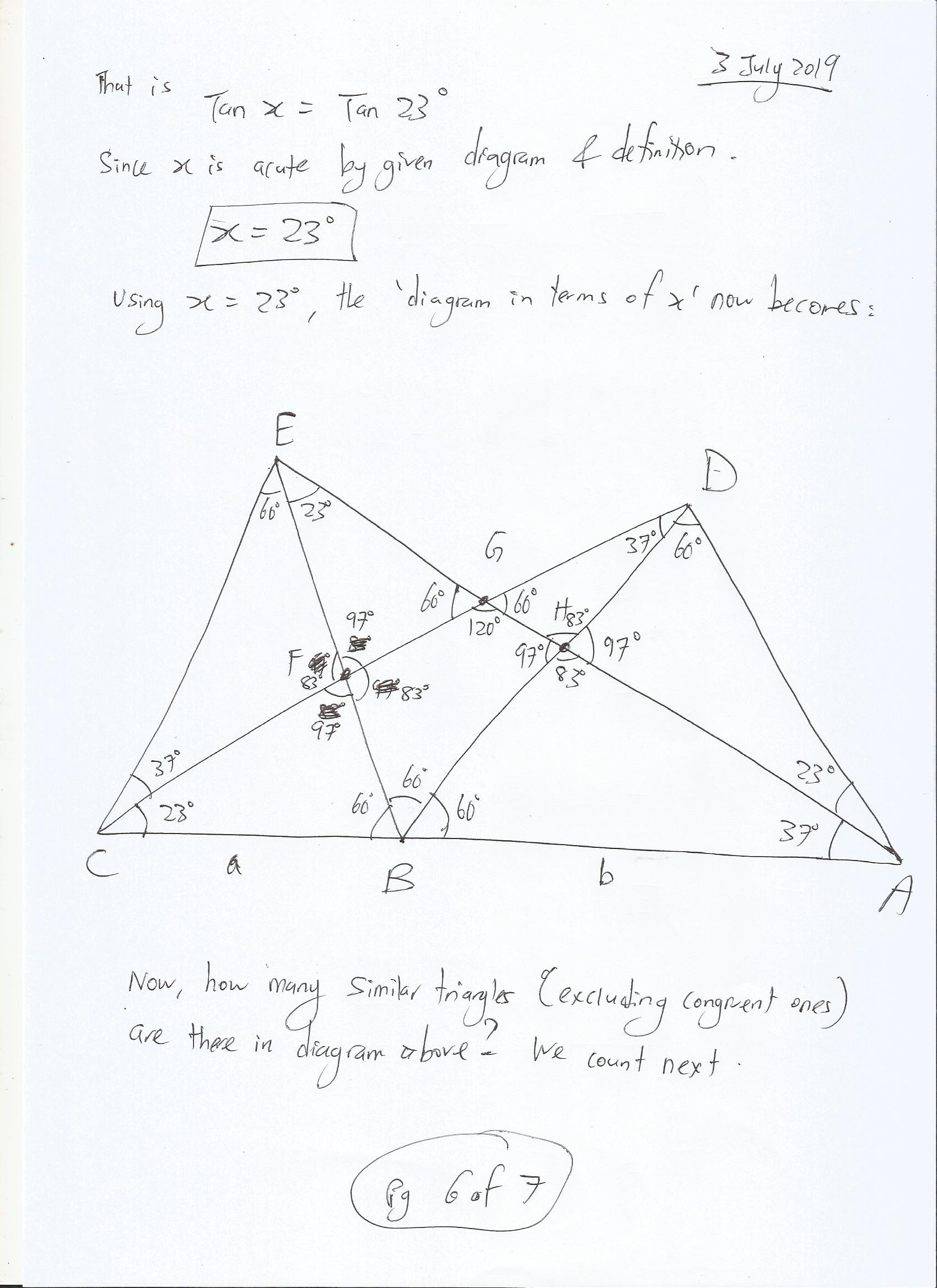

Please remember to teach a person “freely” also in any way you can with your knowledge as a way to Spread Love!
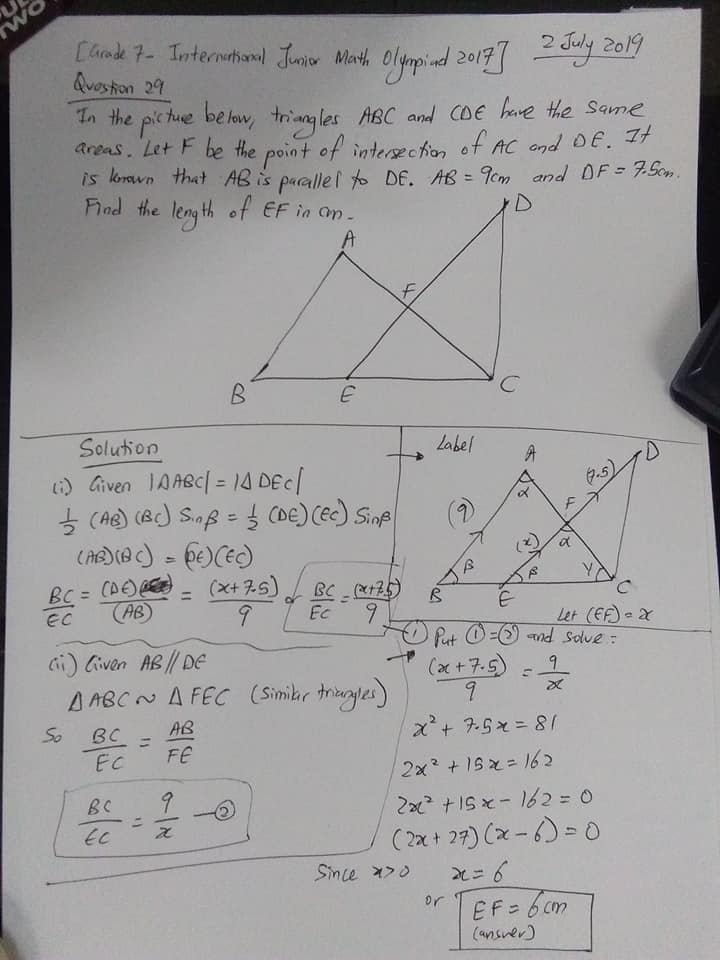
Bonus: Geometry Olympiad – Grade 7 – No. 29 – International Junior Math Olympiad 2017 Question
Geometry – Length and Similar Triangles Ratio with an Equal Area.
Question and a possible Full Solution in image.



Yes, this is a Great Command of the Apostles of the Blessed Lord to ‘remember the poor’ in any way we can, to quote (this Apostolic Exhortation by the ‘Pillars of the Church’):
“(for He who effectually worked for Peter in his apostleship to the circumcised effectually worked for me also to the Gentiles), and recognizing the grace that had been given to me, James and Cephas and John, who were reputed to be pillars, gave to me and Barnabas the right hand of fellowship, so that we might go to the Gentiles and they to the circumcised. They only asked us to remember the poor—the very thing I also was eager to do.” – apostle Paul (Galatians 2:9 – 10, NASB)

Peace to you

STAY CONNECTED